
計量講座:通用計量術(shù)語知識(shí)講座
中國計量科學研究院 施(shī)昌彥
一、測量準確度 是指“測量(liàng)結果與(yǔ)被油量(liàng)真值之(zhī)間的一致程度(dù)”(JJF1001-1998《通用計量術語及定義》規範(fàn)5.5條,以下隻簡條款)。
上述定義中的“一致程度”,不是定量,而(ér)是定性的。關於準確度是一個定(dìng)性概念的問題,可以(yǐ)從以下三個方麵理解。首先,被測量真值其實(shí)就是被測量本身,而與給定的(de)特(tè)定量定義一致的所謂真值,僅是一個理想化(huà)的難以(yǐ)操(cāo)作的概念。因此,不可能準確而定量地給出準確度的值。其次,傳統的誤差理論認為準確度是係統誤差與隨機誤差的綜合,而對它們的合成方法,國際上(shàng)一直沒有統一。最後(hòu),習(xí)慣上所說的準確度其實表示的是不準確的(de)程度,但人們(men)又不願意用貶意的稱謂,而寧可用褒意的稱(chēng)謂。因此在表示(shì)準確(què)度高時,準確度的值(zhí)卻是(shì)更小(xiǎo)。這樣當準確度小於(yú)1%時,究竟是表示誤差小(xiǎo)於1%,還是誤差大於1%?有時讓人搞不(bú)明白引入準確(què)度概念的必要性。
作為曆史形(xíng)成的習慣用語,七個國際組織在1993年規定,沿用的準確(què)度隻是測量結果與被測量真值之間的一致程度或接近程(chéng)度,隻是一個(gè)定性概念,不宜將其定量化。例如:可以定性(xìng)地說“這個研究項目對測量準確度要很高”,“測量準確度應(yīng)滿足使用要求,或某技(jì)術規範、標準的要求”等。換言之(zhī),可以說準確度高低、準確度為0.25級、準確度為3等或準確度符合××標準,而盡量不要說準確度為0.25%、16mg、≤16mg或(huò)±16mg。也就是說,準確度不(bú)宜與數字(zì)相連。若(ruò)需要用數字表示,則可用不確定度。例(lì)如:可以說“測量結果的擴展不確定度為2μΩ”,而不宜說“準確度為2μΩ”。
有些測量儀器(qì)說明書或技(jì)術規範(fàn)中規(guī)定的準確度,其實是儀器的最大允許誤差或允(yǔn)許誤差(chà)極限,不應(yīng)與本定義的測量準確(què)度術語相混淆。測量儀器(qì)的準確度(dù)等級,是它符(fú)合一定的計量要求,使示值(zhí)誤差處於規定極限之內的等別或級別,通常按照約定的方法給這種等級注以數字或(huò)符號。
不要用術(shù)語“精密度”(precision)來表示“準(zhǔn)確度”,因為前者僅反映分散(sàn)性,不能替代後者。精密度的傳統定義是:在規定條件(jiàn)下獲得的各個(gè)獨立觀測值之間的一致程度。所以,精密度僅指由於隨機效應使測量結(jié)果不能完全重複或(huò)複(fù)現,而準確(què)度(dù)則是(shì)指(zhǐ)由於(yú)隨機和係統的綜合效應使測量結果與真值不一(yī)致。實際上,精密度也是一個定性概念,不宜用作定量估計的術語(yǔ)。因為在重複測量條件下的精密(mì)度,可以用測(cè)量結果的重複性(見5.6條)來定量表示;而(ér)在複現測量條件下的精密度,則用(yòng)測量結果的複現性(見5.7條)來定量表示。例如:可以說“測(cè)量結果的重複(fù)性為2mg”或“重複性標(biāo)準〔偏〕差為2mg”,而不宜說“精密度為2mg”。
由於精密度(我國常(cháng)常(cháng)又簡稱為“精度”)一詞用得過泛、過濫,有時甚至並非指傳統定義,因此國際上已回避(bì)使用,七個國際組織也不再沿用。當要定量(liàng)表示或定量估計(jì)測量結果中可能出現的隨機誤差或隨機效應的影響時,可用(yòng)重複性標準〔偏〕差或複現性標準(zhǔn)〔偏〕差(chà)。而過去使用的術語(yǔ)“正確度”(correctness),其實(shí)就是係統誤差或係統效應的影(yǐng)響,它是可以定量表示或定量估計的。
二、[測量結果的]重複性 是指“在相同測量條(tiáo)件下(xià),對(duì)同一被測量進行連續多次測量所得結果之間的一致性”(5.6條)。
上述定義中(zhōng)的“一致性”是定量的,可以用重複性條件下對同(tóng)一量進行(háng)多次(cì)測量所得結果的分散性來表示。而(ér)表示測量結果分散性的量,最為常用(yòng)的是實驗標準〔偏〕差(見5.8條)。在重複性(xìng)條件下按貝塞爾(Bessel)公式算得的實驗標準(zhǔn)〔偏〕差被稱為“重複性標準差”,並記以sr。下(xià)標r被稱為“重複性限(xiàn)”,它是重複性條件下兩次測量結果之差(chà)以95%的概率所存在的區間,即兩次測量結果之差落於r這個區間內或這個差≤r的概(gài)率為95%。假定多次測量所得結果呈正態分布,而且算得的(de)sr充分可靠(自由度(dù)充分大),則可求得![]() ,即重複性限約(yuē)為重複(fù)性標準差的(de)3倍。觀測者通(tōng)常可以利用重複性限,來了解(jiě)測量(liàng)方法導致的不確定度(見5.9條),並用於評定測量結果是否符合要(yào)求。
,即重複性限約(yuē)為重複(fù)性標準差的(de)3倍。觀測者通(tōng)常可以利用重複性限,來了解(jiě)測量(liàng)方法導致的不確定度(見5.9條),並用於評定測量結果是否符合要(yào)求。
重複(fù)性條件包括注2中(zhōng)所列的(de)五個內容。質言之,就(jiù)是在盡量(liàng)相同的條件下,包括程序、人員、儀(yí)器、環境等,以及盡量短的時間間隔(gé)內完成(chéng)重複測量任務。這裏的“短時間”可理(lǐ)解為:保證(zhèng)前四個條件相同或保持不變的時間段,它主要取(qǔ)決於人員的素質、儀器的性能以及對(duì)各種影響量(見(jiàn)4.8條)的監控。從數理(lǐ)統計和數(shù)據處理的角度來看,在這段時(shí)間內測量應處於統計控製狀態,即符合統計(jì)規律的隨機狀態(tài)。通俗地說,它是測量處於正常狀態的時間間隔。重複觀測(cè)中的變動性,正是由於各種影響量(liàng)不能完全(quán)保持恒定而(ér)引(yǐn)起的。重複性標準差有時也稱為組內標準差。
三、[測量結果的(de)]複現性 是指“在改變(biàn)了的測量條件下,同一被測量的測(cè)量結果之間的一致性”(5.7條)。
上述定義的“一致性”是定量的,可以用複現性條件下對同一量進(jìn)行重複測量所得結果的分散性來(lái)表示。這個表示測量結果分散性的量,通常按貝塞爾公式算得,被稱為“複現(xiàn)性標準差”並記以sr。下標r被稱為“複現性限”,其含義類似於5.6條中的(de)重複性限。假定複現性條件是兩個(gè)地(dì)點的不同實驗室,則觀測者(zhě)可以利用複現性限,來(lái)驗證這兩個實驗室之間是否存在過大的係統效應而導致的(de)不確定度。
複現性條件包括注2中所列的八(bā)個內容。這些內容可以改變(biàn)其中一項(xiàng)、多(duō)項或全部。因此,在複現性的有效表述中(zhōng),應說明變化條件(複現性條件)的規範。例如:在(zài)進行校準實驗(yàn)室比(bǐ)對或(huò)能(néng)力驗證試驗(yàn)時,主導實驗(yàn)室將一塊三等標準砝碼逐次送往(wǎng)若幹個參加實驗室,要求各室按(àn)三等標準砝碼檢定規範規定的(de)方法進行測量。這裏,測量原理、測量方法、使用條件沒有改變,但觀測(cè)者、測量儀器(天平)、參考測量(liàng)標準(二等標準砝碼)、地點、時間均發生了改變。
這時對各室得到的測量結果,首先應按各自所用的(de)參考測量標準的修正值(zhí)進(jìn)行相應地修正,然後再按貝塞爾公式計算出sr。此即注4所說的(de)“測量結果在這裏通常理解為已修正結果”。假定按5.6條在(zài)重複性條件(jiàn)下進行若幹次測量,由於在同一個實驗(yàn)室使用的是同一個參考(kǎo)測量(liàng)標準(同一(yī)塊二等標準砝碼),因而在計算sr時就沒有(yǒu)必要按參(cān)考測量標準的修正值進行修正。複現性又稱為再現性。複現性標準差有時也稱為組(zǔ)間標準差。
四、實驗標準[偏]差 是指(zhǐ)“對同一被測量做n次測量,表征測量結果(guǒ)分散性的量s可按下式算出:
![]() 式(shì)中(zhōng):xi為第i次測量的結果;
式(shì)中(zhōng):xi為第i次測量的結果;![]() 為所考慮的n次測量結果的算術平均值”(5.8條(tiáo))。
為所考慮的n次測量結果的算術平均值”(5.8條(tiáo))。
對同一(yī)被測量做有限的n次測(cè)量,其中任何(hé)一次的測量(liàng)結果或觀測值,都可視作無窮多次測量結(jié)果或總體的(de)一個樣本。數理統計方法就是要通過這個樣本所獲(huò)得的信息(例如算術平均值![]() 和實驗標準差s等),來推斷總體的性質(例如期望μ和方差σ2等)。定義注1中指出:當將n個值視作分布的取(qǔ)樣時(shí),x為該(gāi)分大上的期望的無偏差估計,s2為(wéi)該分布的方差σ2的無偏差估計。其中期望是通過無窮多次測量所得的觀測值的(de)算術平均值或加權平均值,又稱為總體均值μ。顯然,它隻是在(zài)理論上存在並可表示為
和實驗標準差s等),來推斷總體的性質(例如期望μ和方差σ2等)。定義注1中指出:當將n個值視作分布的取(qǔ)樣時(shí),x為該(gāi)分大上的期望的無偏差估計,s2為(wéi)該分布的方差σ2的無偏差估計。其中期望是通過無窮多次測量所得的觀測值的(de)算術平均值或加權平均值,又稱為總體均值μ。顯然,它隻是在(zài)理論上存在並可表示為
μ=Lim ∑xi
注1所說的方差σ2,則是無窮多次測量所得觀測值(zhí)xi與期望μ之差的平方(fāng)的(de)算術平均值,它也(yě)隻是在(zài)理論上存在並可表示為
![]() 方差的正平方(fāng)根σ,通常被稱為標準(zhǔn)〔偏〕差,又稱為總體標準(zhǔn)〔偏〕差(chà)(population standard deviation)或理(lǐ)論標準〔偏〕差,而本定義中通過有限次測量求得的實驗標準〔偏〕差s,又稱為樣本標準〔偏〕差(sample standard deviation)。s是σ的估(gū)計值。
方差的正平方(fāng)根σ,通常被稱為標準(zhǔn)〔偏〕差,又稱為總體標準(zhǔn)〔偏〕差(chà)(population standard deviation)或理(lǐ)論標準〔偏〕差,而本定義中通過有限次測量求得的實驗標準〔偏〕差s,又稱為樣本標準〔偏〕差(sample standard deviation)。s是σ的估(gū)計值。
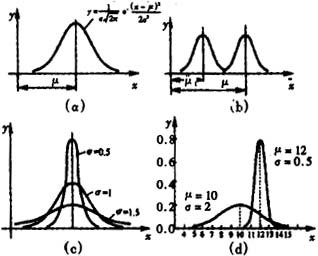
正態分布的總體均值和總體標(biāo)準[偏]差
圖中示出了總體均值為μ,總體標準〔偏〕差為σ的正態分布的情形。由圖(c)可見,σ愈小,分(fèn)布曲線愈集中或愈尖銳,表征測量結果(guǒ)或(huò)觀測值的分散性愈小;反之σ愈大(dà),曲線愈平坦,表征分散性愈大。由圖(a)可見(jiàn),分布曲線在x=μ處具有極大值,曲線不僅是單峰的,而且對x=μ直(zhí)線來說是對稱的,在x=μ±σ處有(yǒu)兩個拐點。由圖(b)可見,分布的中心在x-μ處,μ值的大(dà)小決定了曲線在x軸上的(de)位置(zhì),圖(d)對兩條不同μ值和不同σ值的正態分布曲線進行了比較。
![]() 為μ的無偏估計,s2為(wéi)σ2的無偏估(gū)計(jì)。這裏的“無偏估計”可(kě)理解為:
為μ的無偏估計,s2為(wéi)σ2的無偏估(gū)計(jì)。這裏的“無偏估計”可(kě)理解為:![]() 比μ大(dà)的概率,與
比μ大(dà)的概率,與![]() 比μ小的概率是相等的或皆為50%;而且當n→∞時,(
比μ小的概率是相等的或皆為50%;而且當n→∞時,(![]() -μ)→0。值(zhí)得注意的是:s2為σ2的無偏估計,但s不是σ的無偏估計,而是偏小估(gū)計,即(s-σ)為負值的概率,大於(yú)(s-σ)為正值的概率。
-μ)→0。值(zhí)得注意的是:s2為σ2的無偏估計,但s不是σ的無偏估計,而是偏小估(gū)計,即(s-σ)為負值的概率,大於(yú)(s-σ)為正值的概率。
s是單次觀測值xi的實驗標準〔偏〕差,![]() 才是n次測量所得算術平均值
才是n次測量所得算術平均值![]() 的實驗標準〔偏〕差,它是
的實驗標準〔偏〕差,它是![]() 分(fèn)布的標準(zhǔn)〔偏〕差的估計(jì)值。為易於區別,前者用s(x)表示,後者用s(
分(fèn)布的標準(zhǔn)〔偏〕差的估計(jì)值。為易於區別,前者用s(x)表示,後者用s(![]() )表示,故有s(
)表示,故有s(![]() )=s(x)/
)=s(x)/![]() 。
。
通(tōng)常用s(x)表征測量儀器的重複性,而(ér)用![]() 評價從此儀器進(jìn)行n次測量所得測量結果的(de)分散性。隨著測量次數n的增加,測量結果(guǒ)的分散性
評價從此儀器進(jìn)行n次測量所得測量結果的(de)分散性。隨著測量次數n的增加,測量結果(guǒ)的分散性![]() 即與
即與![]() 成反比地(dì)減小,這是由於對多次觀測值取平(píng)均後,正、負誤(wù)差相互抵償所致。所(suǒ)以,當測(cè)量要求較高或希(xī)望測量結果(guǒ)的標準〔偏差〕較小時,應適當增加n;但是n>20時,隨(suí)著(zhe)n的增加(jiā),
成反比地(dì)減小,這是由於對多次觀測值取平(píng)均後,正、負誤(wù)差相互抵償所致。所(suǒ)以,當測(cè)量要求較高或希(xī)望測量結果(guǒ)的標準〔偏差〕較小時,應適當增加n;但是n>20時,隨(suí)著(zhe)n的增加(jiā),![]() 的減少速率減慢。因此,在選取n的多少(shǎo)時應予綜合考慮或權衡(héng)利弊(bì),因為增加測量次數就(jiù)會拉長測量時間、加大測量成本。在通常情況下,取n≥3,以n=4~20為宜。
的減少速率減慢。因此,在選取n的多少(shǎo)時應予綜合考慮或權衡(héng)利弊(bì),因為增加測量次數就(jiù)會拉長測量時間、加大測量成本。在通常情況下,取n≥3,以n=4~20為宜。
應(yīng)當強調的是:![]() 是平均值的實驗標準〔偏〕差,而不能稱(chēng)它為(wéi)平均值的(de)標(biāo)準誤差。
是平均值的實驗標準〔偏〕差,而不能稱(chēng)它為(wéi)平均值的(de)標(biāo)準誤差。
欄目導(dǎo)航
內(nèi)容推薦(jiàn)
更多(duō)>2019-03-28