計量培（péi）訓：測量不確（què）定度表述講座
國家質量技術監督局　李慎安

　　3.1  實驗（yàn）方差s²(q_k)是方差σ²的無偏估計的（de）含義為何？標準偏差s是否也是總體標準差σ的無偏估計？
　　在用貝塞爾公式
　　計算任一次測量（liàng）結果q_k的實驗標準偏差s(q_k)時，未開方前（qián）以及用本講座2.12問（wèn）題中給出（chū）的式子計算時，未開方前（qián），均稱為實驗方差s²(q_k)。σ稱為總體標準偏差，σ²則稱為總體方差或簡（jiǎn）稱方差，在計量學中（zhōng），特別是測量不確定度評定中，總（zǒng）體是指被測量Y在重複性條件下或複現性條件下無限多次的測量結果（guǒ）。根據這無限多次測量結果（guǒ）計算出（chū）的標準偏差就是σ。由於實驗中，重複的次數n總是有限的（de），計算（suàn）出的實驗方差s²隻是σ²的（de）一個估計值。n越大，這（zhè）個（gè）估計值越可靠。所謂無偏估計，可（kě）以簡單地理解為:s²比σ²大的（de）概率與s²比σ²小的概率相等，即均為50%。而且當次數n越大時，差值(s²-σ²)的總和越趨近為零，當（dāng）n為無窮大時，s²-σ²就等於零。當s²是σ²的無偏估計時（shí），s就不是σ的無偏估（gū）計而是有偏的了，s是σ的偏小估計，即s-σ是負值的概率大於s-σ是正值的概率。在測量不確定度評定中，可以不去考慮這（zhè）種偏小，因為隨n的增大它們會趨於相等。

　　3.2  為什麽在按貝塞爾公式計算的實驗標準偏（piān）差時，次數n應充分大(開方後為什麽隻取正值)複現性條件下的重複測量（liàng）結（jié）果可否采（cǎi）用貝塞爾公式計算一次測量結果的實驗標準偏差？
　　次數n越大，計算出（chū）來的實驗標準偏差s(q_k)越可靠。一般（bān）文獻均提出（chū）應充分大，當然是越大越好，盡可能多地重複測（cè）量。不（bú）過一般來說，次數n≥30就認為充分了。因為（wéi）n等於40或50雖比n=30好一點，但好不了多少。當我們研究測量儀（yí）器（qì）的（de）特性，特（tè）別是其示值分布的（de）情況時，則是另一種目的，次數n往往要超過100甚至200。
　　數字中的平（píng）方根，總是帶有正負（fù）號的（de），例如=±10。但是，在標準差的計（jì）算中，開方後的值隻取正值，原因在於標準差表示的是（shì）分散性，而分散性所給出的是一個（gè）區間或理解為一個範圍。作為物理量的區間的大小，用負值是（shì）沒有意（yì）義的。這（zhè）也就是測量不確定度隻（zhī）有正值（zhí）而（ér）不存（cún）在負值的原因。
　　複現性（xìng）條件下（xià）的重複測量結果之間，也存在分散性，這種條件下的任一（yī）次（cì）測量（liàng）結果（guǒ）的實（shí）驗標準偏差，也無例外地可以用3.1或2.12中給出的式子進行計算。複現性條（tiáo）件似乎不是等精度測量（liàng）所（suǒ）要求（qiú）的（de）條件，但是，所謂等精度（dù）是個定性的概念，重複性條件下的（de）測量結（jié）果有大有小（xiǎo），它們的測量誤差也各不相同，但應該說是有限（xiàn）程度的等精（jīng）度（dù）。複現性條件（jiàn）下出現了某些條（tiáo）件的變化，導致（zhì）測量結果分（fèn）散（sàn）性某種程度的擴大，但仍（réng）可以用實驗標準偏差來定量表述，也可稱之為等精度測量。參閱2.9。

　　3.3  測量不確定度的定義如何理解？
　　測量不確定度定義的英文為:Parameter,associated with the result of a measurement,that characterizes the dispersion of the values that could reasonably be attributed to the measurand。一（yī）般譯為:與測量結（jié）果相聯係的參數，用來表征合理地（dì）賦予被測量之值的分散性。上述譯文把“associated with”譯為“相聯係”不太貼切，英文的含義是“與…一起”，而“相聯係”一詞在漢語中（zhōng），特別是在科技文獻中，往往令人要問，如何聯係，函數形式如何？其實，在這裏測量不確定度與測量結果之間的“聯係”，隻不過是“在一起”，除此以外無其他含義。

　　當我們在重（chóng）複性條件下，對一穩定的被測量X獨立進行了n次重複（fù）測量（liàng），在這一測量列中，通過n個（gè）結果按貝塞爾公式計算出的，第i次（cì）結（jié）果x_i的實驗標準差s(x_i)，與（yǔ）x_i之間有（yǒu）怎樣的聯係？這裏的x_i雖指第i次（cì）測量結（jié）果，而其實際含義則為:任一次的（de）測量結果。因此，s(x_i)=u(x_i)表明這個不確定度(分散性)是這個測量列中任意一次的結果的不確定度。當然，如果（guǒ）在相同的重複性條件下再測一（yī）次，得到的結果x_i的標準不（bú）確定度同樣也是s(x_i)。我們能看（kàn）出這裏的一次測量結果的標準不確定度u(x_i)與x_i之間有怎樣的聯係呢？沒有。

　　怎麽叫合理（lǐ）？怎麽是非合理？在《導則》中未（wèi）予交代。有（yǒu）人說，這裏“合理”一詞妙極，合理就是合理。沒有，也不必要有任何（hé）解釋。隻要賦予被測量之值的分散性不能用不確定度（dù）來表征，則賦予被測量之值就不合理。如果是這樣，我們如何理解不確定度的概念（niàn）呢（ne）？
    定（dìng）義（yì）中所謂的合理，是指（zhǐ）處於統計控製狀態下的測量。當測量是處於統計控製狀態下時，其結果的分散性才能用不（bú）確定度這一參數（shù）表（biǎo）征，否則不（bú）行。
　　國際上對實（shí）驗標準差的定義是表（biǎo）征結果分散性（xìng）的，還有，1994年12月公布的國際標準ISO 5725—《測量方法（fǎ）與測量結（jié）果的準確度》其中對重複性標準差以及複現性（xìng）標準差(s_r與s_R)，都是明確規定重複性條件下和複現性條件下，對同一被測量獨立測量若幹次的測量列，按貝塞爾公式所得到的分散性用標準差定量地給出的值，ISO分別用了標準化的符號s_r與s_R以（yǐ）示區別。
　　所（suǒ）謂統計控（kòng）製狀態的含義，在統計學中就是指隨機（jī）控製過程（chéng）狀態。在計量學中，一般來說，可以具體化為:重複性條件和複現性條（tiáo）件可以保（bǎo）證下的狀態。
　　當我們把測量（liàng）過程中（zhōng）所用的標準測量儀器，按證書所（suǒ）給的修正量或修正曲線，對其（qí）示值(某些情（qíng）況下就是測量結果)進行修正後，由於修（xiū）正值的不（bú）確定度導致的誤差，其期望是可以，而且往（wǎng）往隻能，作為零來估（gū）計的，這就是（shì）一種統計控製狀態，因它（tā）處於隨機過程之中（zhōng）。

　　不確定度是否就是（shì）測量結果的可能誤差？答複是（shì）肯定的。不確定度的（de）含義雖（suī）為賦予被測量之值的分散性（xìng），但是，分散性的形（xíng）成:一是隨機效應；二是係統效應。係統效應導致的誤差分量其期望(指（zhǐ）對那些已知係統誤差進行（háng）過修正後的)與隨（suí）機效（xiào）應導致的誤差分量一樣，都是為零。因此，隻要（yào）沒有遺（yí）漏（lòu）重大的（de）不確定度分量，最後給出的擴展不確定度，無論是（shì）U還是U_p，都是一（yī）種可能誤差(possible error)的量度。事實上，在計量（liàng）學中，過去給測量不（bú）確定度曾經有過一個定義（yì）:由測（cè）量結果所（suǒ）給出的被測量估計值中，可（kě）能誤差的量（liàng）度。這個（gè）定義雖已為1995年的《導則》放棄，但是（shì），其概念與當前所采用（yòng）的定義並不（bú）矛盾，可能（néng）誤差在大多數情況下，表達為一種誤差限，或（huò）最（zuì）大允許誤差等。因此，我們在按檢（jiǎn）定證書或（huò）某（mǒu）些儀器的技術（shù）規範中的這一指標，來估算其所導致的不確定度分量時，就有理由把它們作為（wéi）U或U_p來對待。例如:證書上給出了最大允（yǔn）許誤差不超出±18μA，就可認為U₉₉=18μA。而其（qí）標準不確定（dìng）度在正態分布的前（qián）提下可估算為U₉₉/3=18μA/3=6μA。
　　測量不確定度是否仍可理解為被測（cè）量真值所處範圍的量度？答案也是（shì）肯定的（de），JJF1001-1991中，曾對測量不確（què）定度按當（dāng）時國際上（shàng）的意見定義（yì）為:表征被測量（liàng）的真值所處量值範圍（wéi）的評定（dìng）。這一定義也為國際計量學界所放棄，原因是這兩（liǎng）個定義中均涉及到“真值”、“誤差”這（zhè）樣的理論上的概念而不具有“可操作性”。雖然如此，其所表達的概念並未被國際計量學界所否定。德國於1996年3月所公布的標準DIN1319—3《單一被測量測量結果不確定度的估算》中，對測量不確定（dìng）度的定義卻是（shì）采用（yòng）了:和測量結果一起，用於說明被測量真值所處範圍的（de）一個參數。

　　不確定度與測量結果有多大的聯係？
　　例如:1個三等砝碼，交給某個實驗室，按檢定規程的（de）要求進（jìn）行了測量，得（dé）到其質量為m₁。然後，把這（zhè）個砝碼交給（gěi）另一個實（shí）驗室，同樣按檢定規程進行測量，得（dé）到其質（zhì）量為（wéi）m₂，這兩個實驗室各自使用（yòng）自己（jǐ）的二等標準砝碼與天平，m₁≠m₂是常見的。但是，這（zhè）兩個測量結果的不確定（dìng）度是十分（fèn）接近的，都不超過檢（jiǎn）定規程的三等砝碼的要求（qiú）。因（yīn）此，隻要測量程序、條件相同，不同的測量結果可以有相同的不確定度（dù）。反之，如果測量程序、條件並不相同，雖然測量結果相同，也未必有相（xiàng）同的不（bú）確定度。從這（zhè）個意義上（shàng）來看，測量（liàng）不確定度獨立於測量結果。
　　應該認為:測量不確定度主要決定於測量程序與（yǔ）條（tiáo）件，而測量結果應是這一測量程序與條件下的測量結果而非其他。其聯（lián）係僅此而已。
　　不確定度（dù）指測（cè）量（liàng）結果的可疑程（chéng）度，即對測量結果正確性的可疑程度。其值大則表示不可靠，其值較小，則表示較為可靠，其準確度較高。
　　測量不確定度無例外地隻用正值表述。例如:擴展不確定度U₉₅=0.45 mA。如與測量結果（guǒ）用數學符號聯係起（qǐ）來，則另加正負號(±)。例如:電流I=(70.000±0.054)A。

[page_break]

　　3.4  不確定度分為（wéi）哪些類？
　　不確定度的定義與概念（niàn）已如3.3所述，當（dāng）不確定度除以真值(或測量結果)時（shí），稱（chēng）之為相（xiàng）對不確定度。這是個無量綱量，通（tōng）常（cháng）用百（bǎi）分數或10的負數冪表示(例如10^-6，10^-9)等，而其符號則加下標rel，例如:U_95rel。
　　不（bú）帶形容詞的不確定度指一般概念，當需要明確某一測（cè）量結果的某（mǒu）種不確定度時，要適當（dāng）采用（yòng）一個形容詞，常（cháng）用的形容詞有:標準、擴展(展伸（shēn）或範圍)。在這兩個形容詞前，還（hái）可再加“相對”。例如:相對擴展不（bú）確定度U_rel。
　　當不確定度是用標準偏差表述（shù）時，稱為標準不確定度。
　　當不確定度是采用統計方法(例如用2.12或3.1給出的計算式)得到時，稱A類評定（dìng），而得出的不確定度（dù）稱為A類標準不確定度。當（dāng）用不同於統計（jì）方法的其他方法得到時，稱（chēng）為B類評定，所得出的不確定度稱為B類（lèi）標（biāo）準不確定度（dù）。由各個不確定度的方差和協方（fāng）差之和算出的標準不（bú）確定度，稱為合成標準不確定度，它是測量結果標準偏差的估計。

　　擴展不確定度則（zé）是合成標準不確定度（dù）乘一個包含因子（zǐ）(見3.5)之後擴大了兩倍或兩倍以上的不確（què）定度，它給出的（de）區間能包含被測量可能值的大部分(例如:95%，99%等)。但也可以不必給出其百分數。
　　不確定度的分類可用下圖表明:
    

　　上圖中所給出的各類不確定度均可對（duì）應地給出它們的相對不確定度，即再（zài）除以測量結果。
　　決不可以用隨機不（bú）確定度和係統不確定度這樣的概念和（hé）術語。因不確定度隻是一個分散性區間，這個區間沒有什麽隨機與係統性的問題，更不存在係統的分散性或係統的分散區間。如需要表明某不確定度是怎樣的（de）原（yuán）因所導致的，可以用隨機效應導致（zhì）的不確定度或係統效（xiào）應導致的不確定度，以避免概念上的混淆。必（bì）須注意，隨機效應（yīng）導致的不確定（dìng）度既可以是A類，也可以是B類，而（ér）係統（tǒng）效應導致的不（bú）確（què）定（dìng）度也不一定都是B類。

　　3.5  包含（hán）因子k的概念如何？用在不確定度評定中的什麽場合？
　　包含因子又稱覆蓋因子，它等於（yú）擴展不確定度與合成標準不確定（dìng）度u_c之比。由（yóu）於擴展不確定度（dù）有U與U_p兩類(下標p為置信概率，U_p給出置信概率為p的（de）置信區間半寬)。包含因（yīn）子亦有k與k_p兩（liǎng）類，k與k_p在名稱上沒有區別（bié），使用時，如需區別，必須給出符號。k一般為2，有時為3。而k_p則是在給定（dìng）概（gài）率p時所要求的（de）因子（zǐ），對於被測量Y之估計值接近正態分布的情況下（xià），k_p就是t分布給出的（de）t值。在擴展不確定度U_p的計算中，有了p與自由度ν即可查表得到k_p，從而得到U_p。如隻要求給出擴展不確（què）定度U，則無需k_p而隻用k即（jí）可。

　　3.6  自由度的含（hán）義如何？不確定度評定中起何作用？什麽情（qíng）況（kuàng）下可以不必進行自由度的估算（suàn）？
　　自由度一詞在不同學科有不（bú）同定義，例如在運動學中，指物（wù）體活動空間是幾維。質點隻能沿固定軌道進退為1維，在一個麵上自由運動則是2維，在空間自由運動則是3維，分別稱為自由度等於1，2，3。剛體加上旋轉（zhuǎn）的自由，最大等於6。自（zì）由度從字麵上看是指鬆動程度。計量學（xué）中，如一個被測量（liàng）隻測了一次，有一個結果，不存在選擇（zé）餘地（dì），自由度（dù）為零，但有了兩個測量結果，就多了一（yī）個選擇。不確定度（dù）的評定中，自由度用於表明所得到的標準偏差的可靠程度，它被定義為方差計算中和的項數減（jiǎn）對和的限製數。按貝塞爾公（gōng）式(見3.1)計算方差（chà）s²(q_i)時，∑符號後的項數等於n，因為重複（fù）了n次，被測量Q有（yǒu）n個結（jié）果（guǒ），與其平均值之差就有n個（gè），成為n項之和。但有（yǒu）一（yī）個限製，就是由（yóu）於這n個殘差（chà）之和必為零，即∑(q_i-)=0，這算一個（gè）限製條件。自（zì）由度（dù）ν=n-1。
　　一般，我們可以認為自由度等於（yú）測量次數n減被測量的個數m，即ν=n-m。
　　自由（yóu）度（dù）越大，這個標準差越可靠（kào），自由度ν與這（zhè）個標準差（chà）s的相對不（bú）確定（dìng）度的平方成反比。
　　自由度隻用於包含因子（zǐ）k_p的獲得，如果在擴展不確定度的評定中隻要求U而不是U_p，則（zé）不必進行（háng）自由度的評定及有效自由度的計（jì）算。合成標準不確定度的自由度（dù）稱為有（yǒu）效自由度ν_eff。

　　3.7  置信概率的含義（yì）如何？與置信區間有何關係？
　　按測量不確定度的定義，合理賦予被測量之（zhī）值的分散（sàn）區間是包括全部被測量的測量結果的，即測量結果100%存在於這一區間。這一分散區間的半寬一般用（yòng）a表示。但是如（rú）隻要（yào）求（qiú）某個區間隻包含其95%的賦予被測量之值（zhí），這個區（qū）間就稱為（wéi）概率p=95%的置信區間，其半寬就是擴展不確定度U₉₅，如要求99%的概率，則為U₉₉。相（xiàng）應的概率（lǜ）稱為置信概率，有:
　　U₉₅<U₉₉<a
　　至於大多少，與賦予被（bèi）測量之值的分（fèn）布（bù）情（qíng）況有關。

　　3.8  測量（liàng）誤差的定義、分類以及使用時應注（zhù）意哪些問題？
　　測量誤差(簡稱誤差)的定（dìng）義從20世（shì）紀70年代（dài）以來沒有改變，定義為:測量結（jié）果減（jiǎn）被測量（liàng）的真值。但是，長期（qī）以來，國（guó）內外計量學界常錯誤地使（shǐ）用誤差一詞。從定義看，誤差與測量結果有關而與測量方法無關。不同的測量結果有不同誤差，相同測量結（jié）果有相同誤差（chà），而（ér）不論測量（liàng）結果是來自何種測（cè）量方法。合理賦予被測量之值，各（gè）有其（qí）誤差而並不存在一個共同的誤差。一個測量結果的誤差，如不是（shì）正值就是負值，取（qǔ）決於這個結果是大於還是小於真值。因此，誤差（chà）決不（bú）會帶有正負號(±)。
　　測量結果的誤差往往由（yóu）若幹分量組成，這些分量按其特性分成隨機（jī）誤差與（yǔ）係統誤差兩大（dà）類，而測量（liàng）結果的誤（wù）差無例外地是全部分量的代數和（hé）。即，對誤差的合成隻有代（dài）數和這一種方式。
　　隨（suí）機誤差（chà）的定義在1993年以來作了原則性的改變，它被定義為:測量結果減重複性條件對同一量進行無限多次測量結果的平均值。測量（liàng）結果是真（zhēn）值、係統誤差與隨機誤差這三者的代數和（hé），而無限多次結果的平均值則隻是真值與係統誤差的代數和。它們的差則是（shì）這一測量結果的隨機誤差分量。
　　注意:不再（zài）有（yǒu）偶然誤差這一術語，也不再（zài）有另外的定義。

　　係統誤差也有了原則性的改變，它被定義為:重複性條件下對被測量的（de）無（wú）限多次測量結果的算（suàn）術平均值減被測量的真值。由於隻能有限次數的重（chóng）複，而真值隻（zhī）能（néng）用給定真值代替，因此，所得到的係統誤差隻是個估計值，並具有一定的不確定度。這個不確定（dìng）度也就是修正值的不確（què）定度，與其他來源的不確（què）定度分量一樣進入合成（chéng）標準不確定度，僅此而已。而不是把係統誤（wù）差分成為已知係統誤差和未知係統誤差，也不能說未知係統誤差按隨機誤差處理。因為這裏（lǐ）所謂的未知係統誤差並非誤差分量而是不確定度（dù），而且，所謂按隨機誤差處理，概念（niàn）是不清的（de）。
　　至於誤差限、最大允（yǔn）許（xǔ）誤差、可能誤差、引用誤差等術語，它們前麵帶有正負號(±)，是一種（zhǒng）可能誤差的分散區間，而（ér）並非一（yī）個（gè）測量結果的誤差。
　　過去所謂的（de）誤差傳播定律，所傳播者並非誤差而是不確定度。現在（zài）已改稱為不確定度傳播定律。
　　應該注意，誤差一詞（cí）隻能按（àn）其定義使用。今後不應用（yòng）它（tā）來定量表（biǎo）明測量結果（guǒ）的可靠程度。

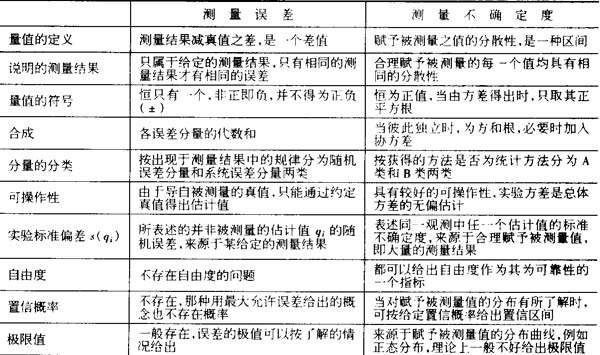
　　3.9  測量誤差與測量不確定度之間（jiān）存在哪些主要不同之處？
　　下表給出它們之（zhī）間的主要不（bú）同之處（chù）:

　　3.10  什麽叫變量之間的相關？如何定量表達？不確定度評定中如何給出其估計值，什麽情況（kuàng）下發生相關？有沒有B類估算（suàn）？
　　一切被測量的估計值，由於諸多不穩定因素（sù）的影響，它們不是固定的，因而稱之為變量。也就是說量的測量結果都是變量。
　　當某些被測量的估計值有相同的不確定度來源，特別是（shì）受相同的係（xì）統效應的影響（xiǎng），例如用了同一（yī）個標準器，則這樣的變量間存在相關。均可能偏大或（huò）均可能偏小，稱為正相關；一個偏大而另（lìng）一個偏小，稱為負（fù）相關。這種相關性導（dǎo）致的方差稱為協方差，進入合成方差的（de）計算，從而擴大（dà）了所得的合成方差(合成方差是合成標準（zhǔn）差（chà）的二次方)。
　　協方差的評定（dìng）既有A類評定也有B類評定。往往也可通過測量的操作（zuò）程序來避免相關的產生，即使其協方差小到可忽略不計，例如通過改變所用的標準（zhǔn）器等。